Konsep penting dalam kalkulus adalah rate of change, apa itu?#

Pengukuran laju perubahan (rate of change) adalah konsep integral dalam kalkulus diferensial, yang berkaitan dengan matematika perubahan dan infinitesimal. Konsep ini memungkinkan kita untuk menemukan hubungan antara dua variabel yang berubah dan bagaimana hal ini mempengaruhi satu sama lain.

Pengukuran laju perubahan juga penting untuk pembelajaran mesin, seperti dalam menerapkan gradient descent sebagai algoritma pengoptimalan untuk melatih model jaringan saraf.

Dalam tutorial ini, Anda akan menemukan laju perubahan sebagai salah satu konsep utama dalam kalkulus, dan pentingnya mengukurnya.

Setelah menyelesaikan tutorial ini, Anda akan tahu:

• Bagaimana laju perubahan fungsi linear dan non-linear diukur.
• Mengapa pengukuran laju perubahan merupakan konsep penting dalam berbagai bidang.

Mari kita mulai. Tutorial ini dibagi menjadi dua bagian, yaitu:

• Laju Perubahan
• Pentingnya Mengukur Laju Perubahan

Laju Perubahan atau Rate of Change#

Laju perubahan mendefinisikan hubungan antara satu variabel yang berubah dengan variabel lainnya.

Pertimbangkan sebuah benda bergerak yang berpindah dua kali lebih banyak ke arah vertikal, dilambangkan dengan y, daripada ke arah horizontal, dilambangkan dengan x. Dalam istilah matematis, hal ini dapat dinyatakan sebagai:

$\Delta y = 2 \Delta x$

Huruf Yunani delta $\Delta$ sering digunakan untuk menunjukkan perbedaan atau perubahan. Oleh karena itu, persamaan di atas mendefinisikan hubungan antara perubahan dalam posisi x sehubungan dengan perubahan dalam posisi y dari objek yang bergerak.

Perubahan arah x dan y ini dapat digambarkan dengan garis lurus pada sistem koordinat x-y. Dalam representasi grafis pergerakan objek ini, laju perubahan diwakili oleh kemiringan garis, atau gradiennya. Karena garis terlihat naik 2 unit untuk setiap unit yang bergerak ke kanan, maka laju perubahannya, atau kemiringannya, sama dengan 2.

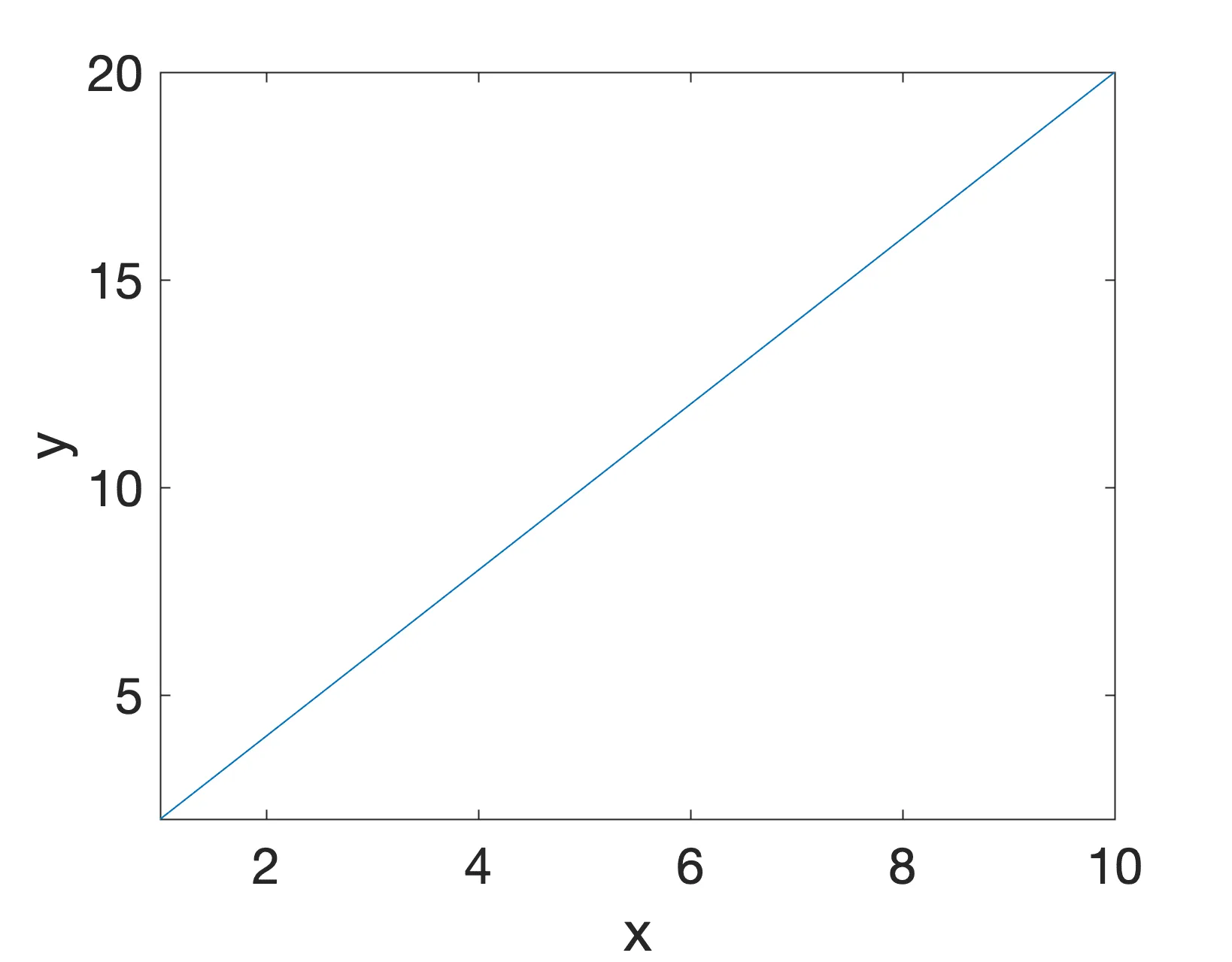
Dengan menyatukan semuanya, kita bisa melihatnya:

$rate\ of\ change = \frac{\Delta y}{\Delta x} = kemiringan$

Jika kita harus mempertimbangkan dua titik tertentu, $P_1 = (2, 4)$ dan $P_2 = (8, 16)$, pada garis lurus ini, kita dapat mengkonfirmasi kemiringannya sama dengan:

$kemiringan = \frac{\Delta y}{\Delta x} = \frac{16 - 4}{8 - 2} = \frac{12}{6} = 2$

Untuk contoh khusus ini, laju perubahan, yang diwakili oleh kemiringan, adalah positif karena arah garis meningkat ke kanan. Namun, laju perubahan juga dapat bernilai negatif jika arah garis menurun, yang berarti bahwa nilai y akan menurun ketika nilai x meningkat. Lebih jauh lagi, ketika nilai y tetap konstan ketika x meningkat, kita dapat mengatakan bahwa kita memiliki laju perubahan nol. Sebaliknya, jika nilai x tetap konstan seiring dengan meningkatnya nilai y, kita akan menganggap rentang perubahannya tidak terbatas, karena kemiringan garis vertikal dianggap tidak terdefinisi.

Sejauh ini, kita telah mempertimbangkan contoh paling sederhana dari sebuah garis lurus, dan karenanya merupakan fungsi linier, dengan kemiringan yang tidak berubah. Meskipun demikian, tidak semua fungsi sesederhana ini, dan jika memang demikian, maka tidak perlu kalkulus. Oleh karena itu, kita perlu mempertimbangkan fungsi yang lebih kompleks, yang dapat menggambarkan hubungan antara dua variabel yang berubah.

Mari kita pertimbangkan sebuah fungsi non-linear sederhana, parabola:

$y = \frac{1}{4}x^2$

Berbeda dengan kemiringan konstan yang menjadi ciri garis lurus, kita dapat melihat bagaimana parabola ini menjadi lebih curam dan lebih curam saat kita bergerak ke kanan. Oleh karena itu, kita dapat mengatakan bahwa laju perubahan fungsi ini meningkat seiring dengan meningkatnya nilai x. Dengan kata lain, laju perubahan fungsi ini adalah fungsi dari x.

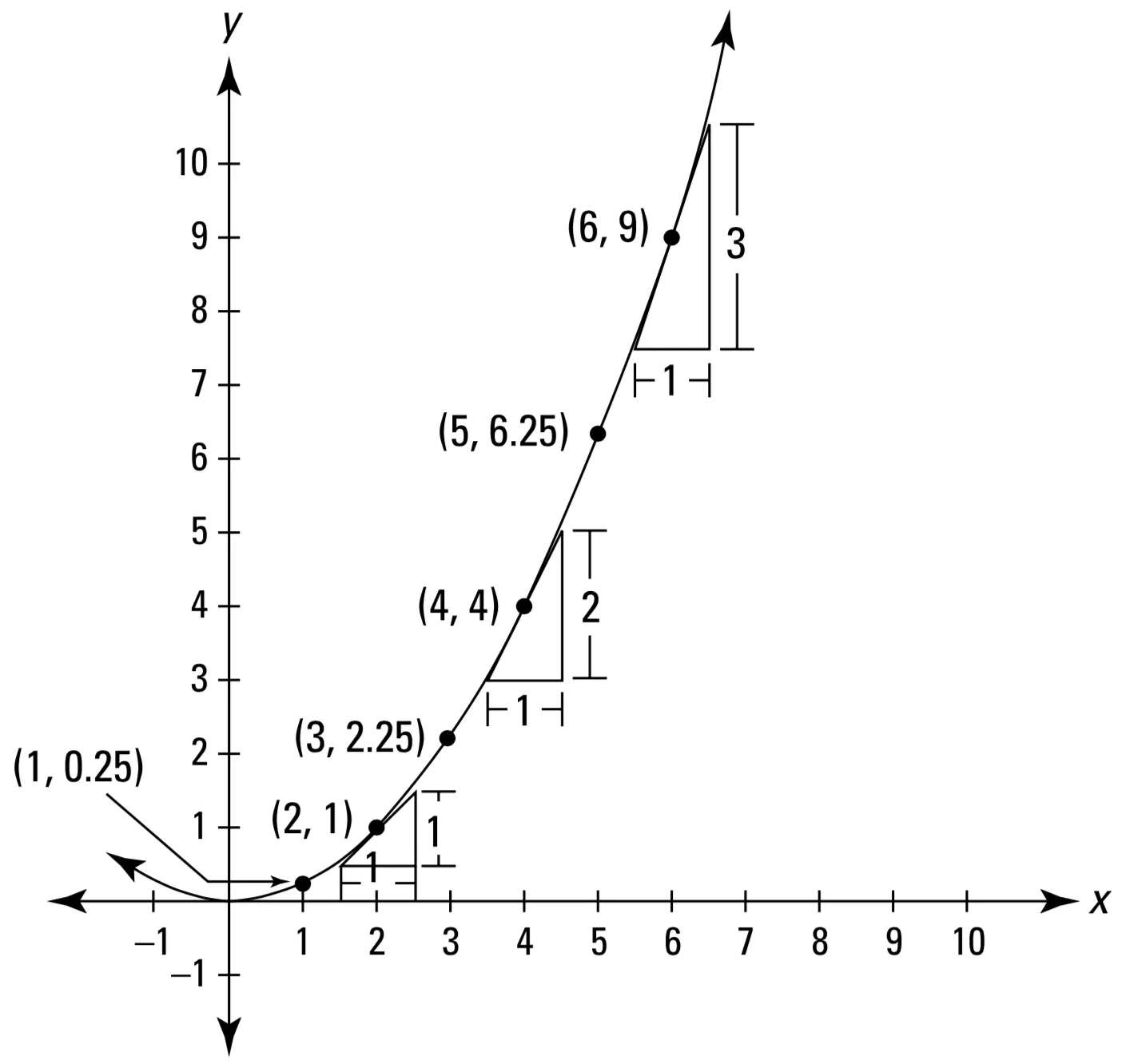
Ingatlah bahwa metode kalkulus memungkinkan kita untuk menganalisis bentuk lengkung dengan memotongnya menjadi banyak potongan lurus tak terhingga yang disusun berdampingan. Jika kita harus mempertimbangkan salah satu dari potongan tersebut pada titik tertentu, P, pada bentuk lengkung parabola, kita akan melihat bahwa kita harus menghitung lagi laju perubahan sebagai kemiringan garis lurus. Penting untuk diingat bahwa laju perubahan pada parabola bergantung pada titik tertentu, P, yang kebetulan kita pertimbangkan sejak awal.

Sebagai contoh, jika kita harus mempertimbangkan garis lurus yang melewati titik, P = (2, 1), kita akan menemukan bahwa laju perubahan pada titik ini pada parabola adalah:

$kemiringan = \frac{\Delta y}{\Delta x} = \frac{1}{1} = 1$

kalau pada titik, P = (6, 9), kita akan menemukan bahwa laju perubahan pada titik ini pada parabola adalah:

$kemiringan = \frac{\Delta y}{\Delta x} = \frac{3}{1} = 3$

Garis lurus yang menyentuh kurva sebagai titik tertentu, P, dikenal sebagai garis singgung, sedangkan proses menghitung laju perubahan suatu fungsi juga dikenal sebagai mencari turunannya.

Meskipun kita telah mempertimbangkan parabola sederhana untuk contoh ini, kita juga dapat menggunakan kalkulus untuk menganalisis fungsi non-linear yang lebih rumit. Konsep penghitungan laju perubahan sesaat pada titik-titik tangensial yang berbeda pada kurva tetap sama.

Kita akan menemukan salah satu contohnya ketika kita akan melatih jaringan syaraf menggunakan algoritma gradient descent. Sebagai algoritma optimasi, gradient descent secara iteratif menurunkan fungsi kesalahan menuju minimum globalnya, setiap kali memperbarui bobot jaringan syaraf untuk memodelkan data pelatihan dengan lebih baik. Fungsi kesalahan biasanya non-linear dan dapat mengandung banyak titik minimum dan sadel lokal. Untuk menemukan jalan menurun, algoritma gradient descent menghitung kemiringan sesaat pada titik-titik yang berbeda pada fungsi kesalahan, hingga mencapai titik di mana kesalahan paling rendah dan tingkat perubahannya nol.

Mengapa pengukuran laju perubahan merupakan konsep penting dalam berbagai bidang#

Sejauh ini, kita telah mempertimbangkan laju perubahan per unit pada sistem koordinat x-y. Dalam konteks pelatihan jaringan saraf, misalnya, kita telah melihat bahwa gradien kesalahan dihitung sebagai perubahan kesalahan sehubungan dengan bobot tertentu dalam jaringan saraf.

Ada banyak bidang yang berbeda di mana pengukuran laju perubahan merupakan konsep yang penting juga. Beberapa contohnya adalah:

• Dalam fisika, kecepatan dihitung sebagai perubahan posisi per satuan waktu.
• Dalam digitalisasi sinyal, laju pengambilan sampel dihitung sebagai jumlah sampel sinyal per detik.
• Dalam komputasi, kecepatan bit adalah jumlah bit yang diproses komputer per satuan waktu.
• Dalam keuangan, nilai tukar mengacu pada nilai satu mata uang terhadap mata uang lainnya.

Kesimpulan#

Dalam tutorial ini, Anda menemukan laju perubahan sebagai salah satu konsep utama dalam kalkulus, dan pentingnya mengukurnya.

Secara khusus, Anda telah belajar:

• Pengukuran laju perubahan adalah konsep integral dalam kalkulus diferensial yang memungkinkan kita untuk menemukan hubungan antara satu variabel yang berubah dengan variabel lainnya.
• Ini adalah konsep penting yang dapat diterapkan pada banyak bidang, salah satunya adalah pembelajaran mesin.