Kalkulus pada machine learning#

Calculus adalah salah satu konsep matematika inti dalam pembelajaran mesin yang memungkinkan kita untuk memahami kerja internal dari berbagai algoritma pembelajaran mesin.

Salah satu aplikasi penting dari kalkulus dalam pembelajaran mesin adalah algoritma gradient descent, yang, bersama dengan backpropagation, memungkinkan kita untuk melatih model jaringan saraf.

Dalam tutorial ini, Anda akan menemukan peran integral dari kalkulus dalam pembelajaran mesin.

Setelah menyelesaikan tutorial ini, Anda akan tahu:

• Calculus memainkan peran penting dalam memahami fungsi internal algoritma pembelajaran mesin, seperti algoritma gradient descent untuk meminimalkan fungsi kesalahan.
• Calculus menyediakan alat yang diperlukan untuk mengoptimalkan fungsi objektif yang kompleks serta fungsi dengan input multidimensi, yang merupakan representasi dari berbagai aplikasi pembelajaran mesin.

Mari kita mulai. Tutorial ini dibagi menjadi dua bagian, yaitu:

• Penggunaan Calculus dalam Machine Learning
• Bagaimana Calculus dalam Machine Learning Bekerja

Calculus pada Machine Learning#

Sebuah model neural network, baik shallow atau deep, mengimplementasikan fungsi yang memetakan serangkaian input ke output yang diharapkan. Fungsi yang diimplementasikan oleh neural network dipelajari melalui proses training, yang secara iteratif mencari seperangkat beban (weights) yang paling memungkinkan neural network untuk memodelkan variasi dalam data training.

Fungsi linear seperti itu dapat diwakili oleh persamaan garis yang memiliki slope, m, dan y-intercept, c:

$y = mx + c$

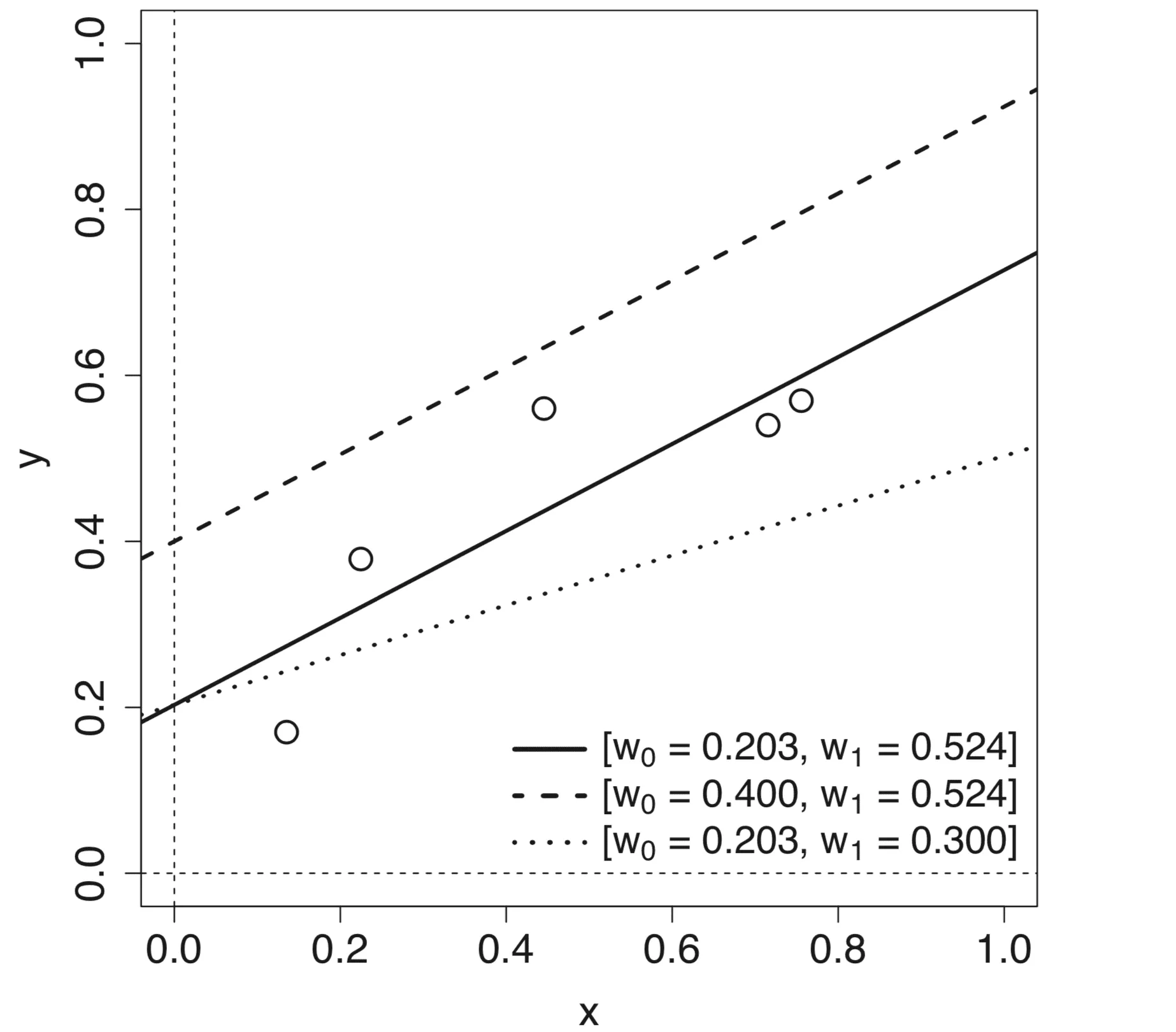
Banyaknya hasil variasi masing-masing parameter, m dan c, menghasilkan model linear yang berbeda yang mendefinisikan peta input-output yang berbeda.

Oleh karena itu, proses pembelajaran fungsi pemetaan melibatkan perkiraan parameter model ini, atau bobot, yang menghasilkan kesalahan minimum antara output yang diprediksi dan target. Kesalahan ini dihitung dengan menggunakan fungsi kerugian, fungsi biaya, atau fungsi kesalahan, yang sering digunakan secara bergantian, dan proses meminimalkan kerugian disebut sebagai optimasi fungsi.

Kita dapat menerapkan kalkulus diferensial pada proses optimasi fungsi. Untuk lebih memahami bagaimana kalkulus diferensial dapat diterapkan pada optimasi fungsi, mari kita kembali ke contoh spesifik kita tentang fungsi pemetaan linear.

Katakanlah kita memiliki beberapa kumpulan data fitur input tunggal, x, dan target output yang sesuai, y. Untuk mengukur kesalahan pada kumpulan data tersebut, kita akan menggunakan jumlah kesalahan kuadrat (SSE), yang dihitung antara output yang diprediksi dan target, sebagai fungsi kerugian.

Melakukan penyisiran parameter pada nilai yang berbeda untuk bobot model, w0 = m dan w1 = c, menghasilkan profil kesalahan individu yang berbentuk cembung.

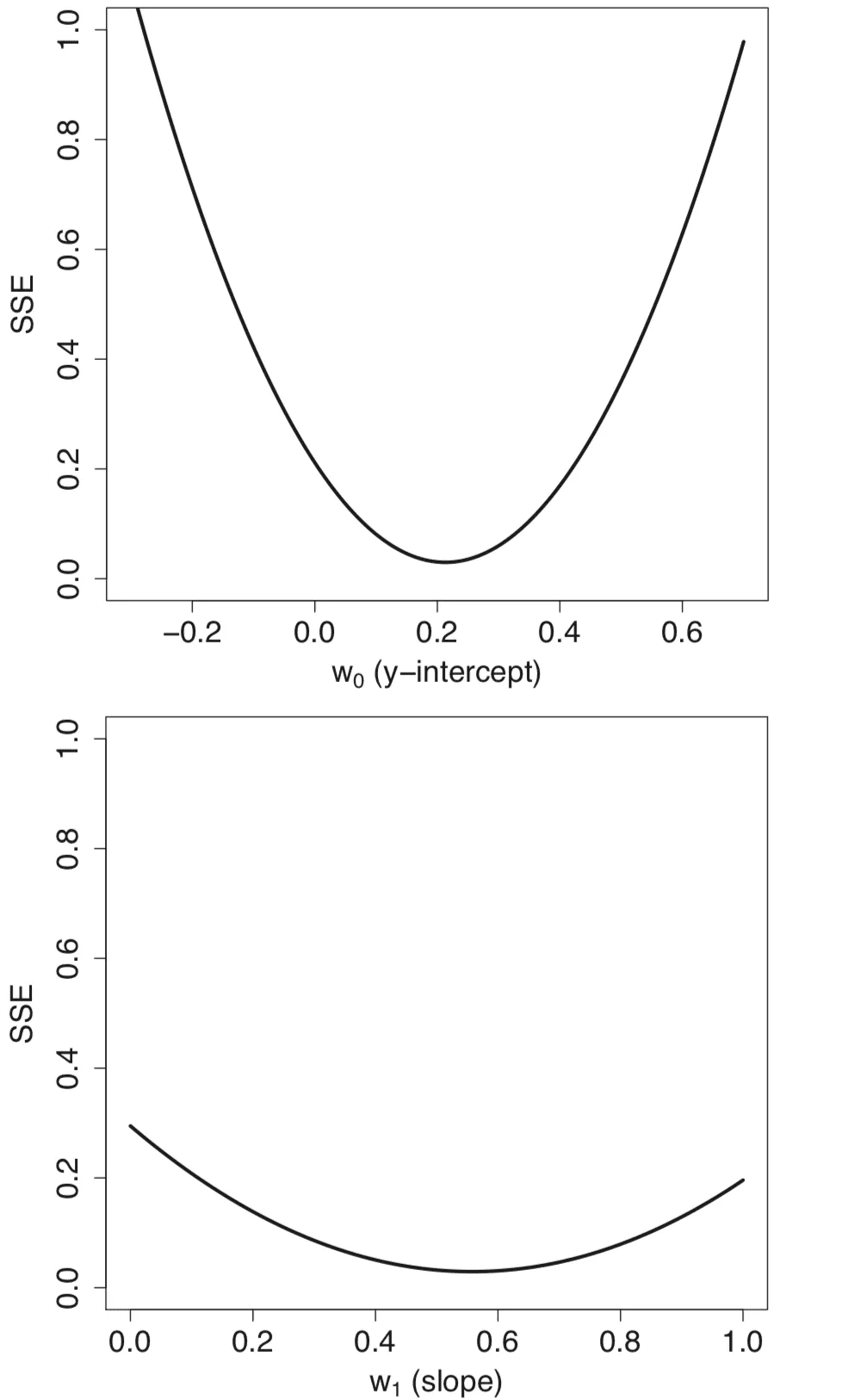
Menggabungkan profil error individu menghasilkan permukaan error tiga dimensi yang juga berbentuk cembung. Permukaan error ini terkandung dalam ruang bobot, yang didefinisikan oleh rentang nilai yang disapu untuk bobot model, w0 dan w1.

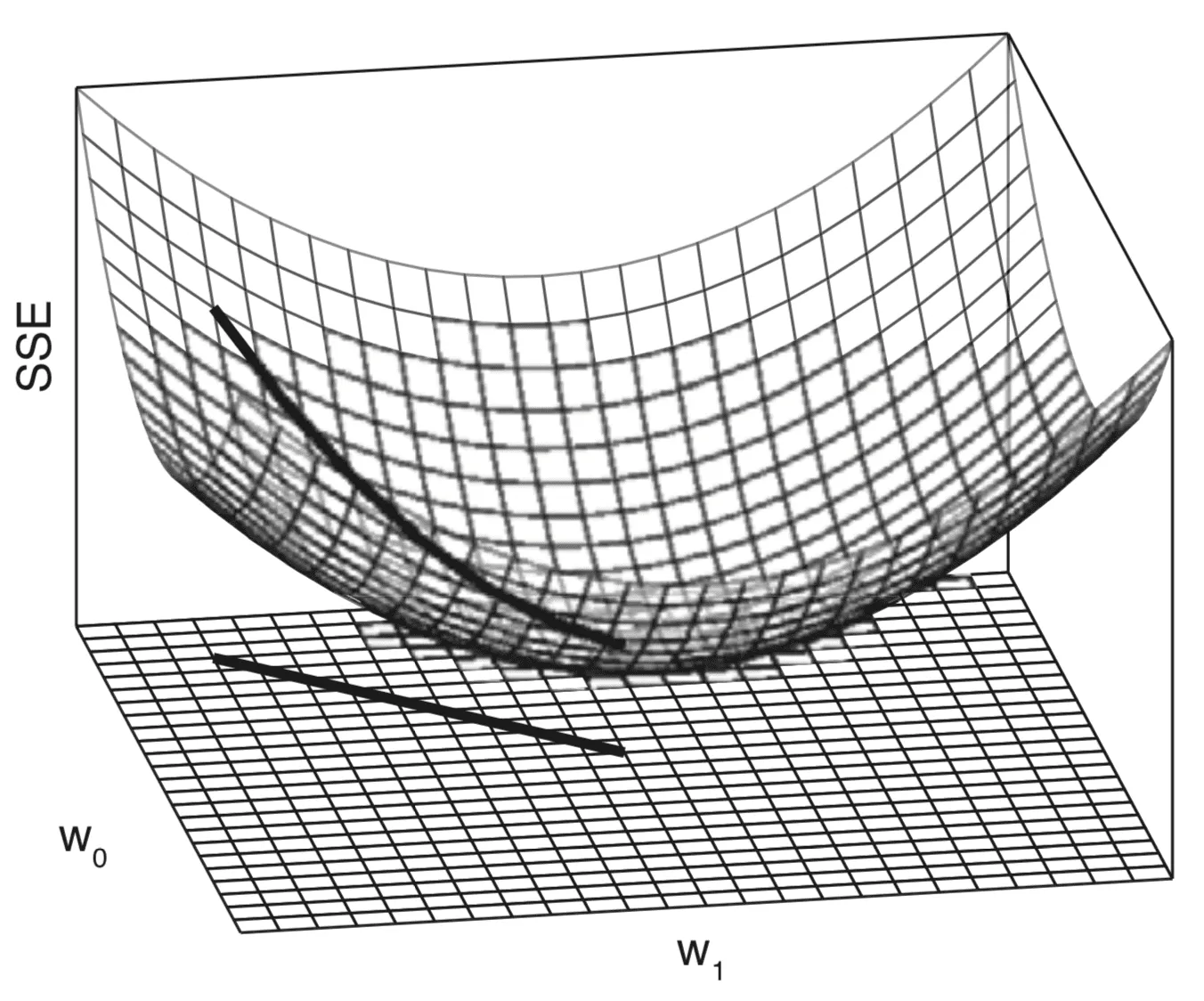
Bergerak melintasi ruang bobot ini setara dengan bergerak di antara model linier yang berbeda. Tujuan kami adalah untuk mengidentifikasi model yang paling sesuai dengan data di antara semua alternatif yang ada. Model terbaik ditandai dengan error terendah pada dataset, yang sesuai dengan titik terendah pada permukaan error.

Algoritma gradient descent, sebagai algoritma optimasi, akan berusaha mencapai titik terendah pada permukaan error dengan mengikuti gradiennya menurun. Penurunan ini didasarkan pada perhitungan gradien, atau kemiringan, dari permukaan error. Di sinilah kalkulus diferensial berperan. Secara lebih formal, mari kita tunjukkan fungsi yang ingin kita optimalkan:

$error = f(w0, w1)$ or $error = f(all\ weight)$

Dengan menghitung tingkat perubahan, atau kemiringan, error sehubungan dengan bobot, algoritma gradient descent dapat memutuskan bagaimana cara mengubah bobot untuk terus mengurangi error.

Bagaimana Calculus dalam Machine Learning Bekerja#

Fungsi kesalahan yang telah kita pertimbangkan untuk dioptimalkan relatif sederhana, karena cembung dan ditandai dengan satu minimum global. Meskipun demikian, dalam konteks pembelajaran mesin, kita sering kali perlu mengoptimalkan fungsi yang lebih kompleks yang dapat membuat tugas pengoptimalan menjadi sangat menantang. Optimasi dapat menjadi lebih menantang jika input ke fungsi juga multidimensi.

Kalkulus memberi kita alat yang diperlukan untuk mengatasi kedua tantangan tersebut. Misalkan kita memiliki fungsi yang lebih umum yang ingin kita minimalkan, dan yang membutuhkan input nyata, x, untuk menghasilkan output nyata, y:

$y = f(x)$

Menghitung laju perubahan pada nilai x yang berbeda sangat berguna karena memberikan indikasi perubahan yang perlu kita terapkan pada x, untuk mendapatkan perubahan yang sesuai pada y.

Karena kita meminimalkan fungsi, tujuan kita adalah untuk mencapai titik yang mendapatkan nilai f(x) serendah mungkin yang juga ditandai dengan laju perubahan nol; oleh karena itu, minimum global. Tergantung pada kompleksitas fungsi, hal ini belum tentu dapat dilakukan karena mungkin ada banyak titik minimum lokal atau titik pelana yang mungkin masih terjebak dalam algoritma optimasi. Oleh karena itu, dalam konteks deep learning, kita sering menerima solusi suboptimal yang mungkin tidak selalu sesuai dengan nilai minimum global, selama solusi tersebut sesuai dengan nilai f(x) yang sangat rendah.

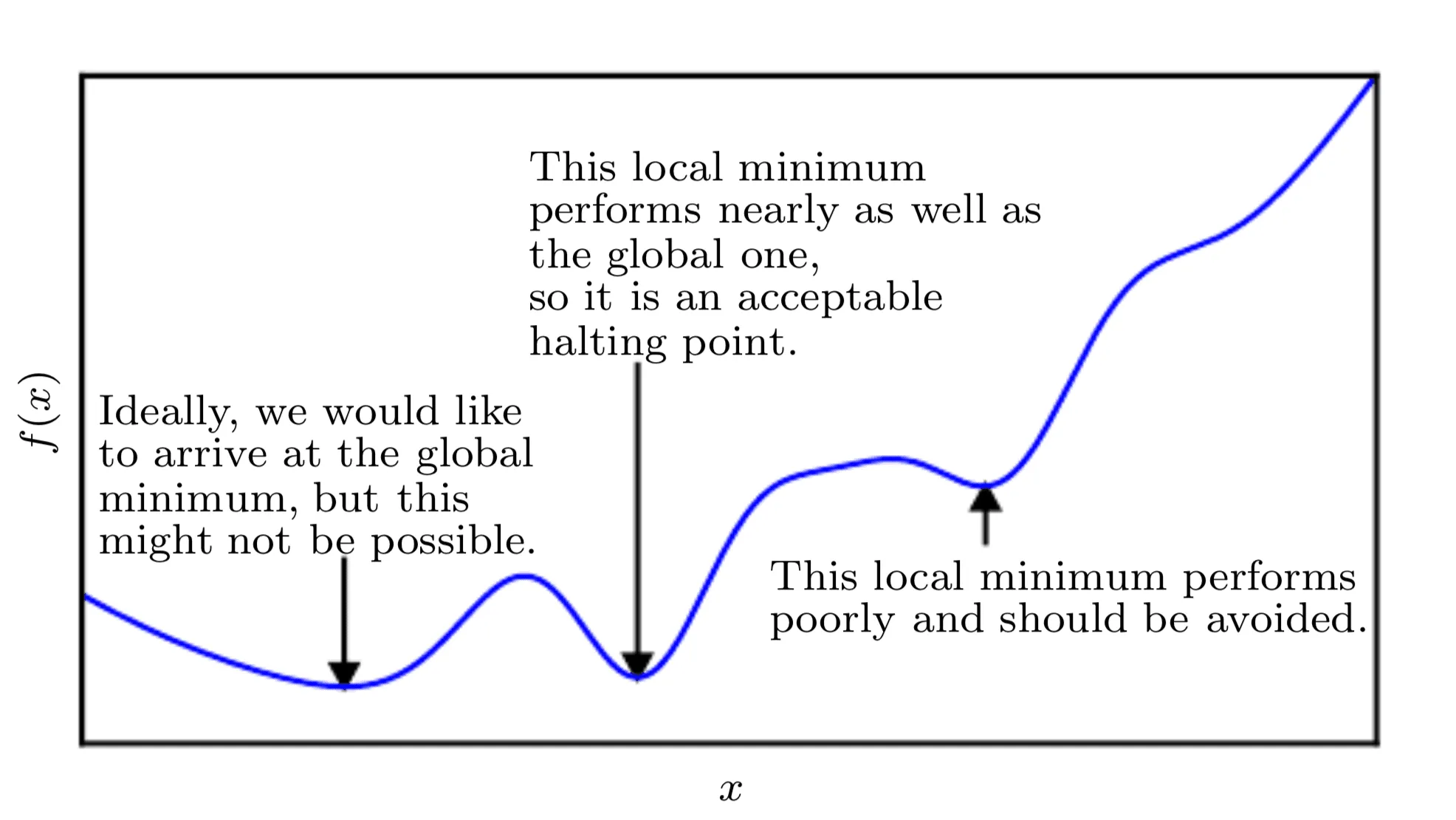
Jika fungsi yang kita kerjakan membutuhkan banyak input, kalkulus juga menyediakan konsep turunan parsial; atau dalam istilah yang lebih sederhana, sebuah metode untuk menghitung laju perubahan y sehubungan dengan perubahan pada setiap input, xi, dengan tetap mempertahankan input yang lain tetap konstan.

Oleh karena itu, jika kita mempertimbangkan lagi minimalisasi fungsi kesalahan, menghitung turunan parsial untuk kesalahan sehubungan dengan setiap bobot tertentu memungkinkan setiap bobot diperbarui secara independen dari yang lain.

Hal ini juga berarti bahwa algoritma gradient descent mungkin tidak mengikuti jalur lurus ke bawah permukaan kesalahan. Sebaliknya, setiap bobot akan diperbarui secara proporsional dengan gradien lokal dari kurva kesalahan. Oleh karena itu, satu bobot dapat diperbarui dengan jumlah yang lebih besar dari yang lain, sebanyak yang dibutuhkan algoritma gradient descent untuk mencapai fungsi minimum.

Summary#

Dalam tutorial ini, Kita telah menemukan peran integral kalkulus dalam pembelajaran mesin. Secara khusus, Kita telah belajar:

• Kalkulus memainkan peran integral dalam memahami cara kerja internal algoritma pembelajaran mesin, seperti algoritma gradient descent yang meminimalkan fungsi kesalahan berdasarkan perhitungan laju perubahan.
• Konsep laju perubahan dalam kalkulus juga dapat dieksploitasi untuk meminimalkan fungsi objektif yang lebih kompleks yang tidak selalu berbentuk cembung.
• Perhitungan turunan parsial, konsep penting lainnya dalam kalkulus, memungkinkan kita untuk bekerja dengan fungsi yang menerima banyak input.