Jaringan syaraf tiruan adalah model komputasi yang mendekati pemetaan antara input dan output. Model ini terinspirasi oleh struktur otak manusia, yang juga terdiri dari jaringan neuron yang saling terhubung yang menyebarkan informasi setelah menerima serangkaian rangsangan dari neuron di sekitarnya.

Melatih neural network melibatkan proses yang menggunakan algoritme backpropagation dan gradient descent secara bersamaan. Seperti yang akan kita lihat, kedua algoritma ini menggunakan kalkulus secara ekstensif.

Dalam tutorial ini, Anda akan menemukan bagaimana aspek kalkulus diterapkan dalam jaringan syaraf tiruan.

Setelah menyelesaikan tutorial ini, Anda akan tahu:

• Jaringan syaraf tiruan disusun ke dalam lapisan-lapisan neuron dan koneksi, di mana setiap lapisan diberi nilai bobot.
• Setiap neuron mengimplementasikan fungsi nonlinier yang memetakan satu set input ke activation output.
• Dalam melatih neural network, kalkulus digunakan secara ekstensif oleh algoritme backpropagation dan gradient descent.

Mari kita mulai. Tutorial ini dibagi menjadi tiga bagian, yaitu:

• Pengantar ke Jaringan Syaraf Tiruan
• Matematika dari sebuah Neuron
• Melatih Jaringan

Pengenalan Neural Networks#

Jaringan syaraf tiruan dapat dianggap sebagai algoritma aproksimasi fungsi. Dalam pengaturan pembelajaran yang diawasi, ketika disajikan dengan banyak pengamatan input yang mewakili masalah yang diminati, bersama dengan target output yang sesuai, neural network akan berusaha memperkirakan pemetaan yang ada di antara keduanya.

Otak manusia terdiri dari jaringan besar neuron yang saling terhubung (sekitar seratus miliar neuron), yang masing-masing terdiri dari badan sel, seperangkat serat yang disebut dendrit, dan akson:

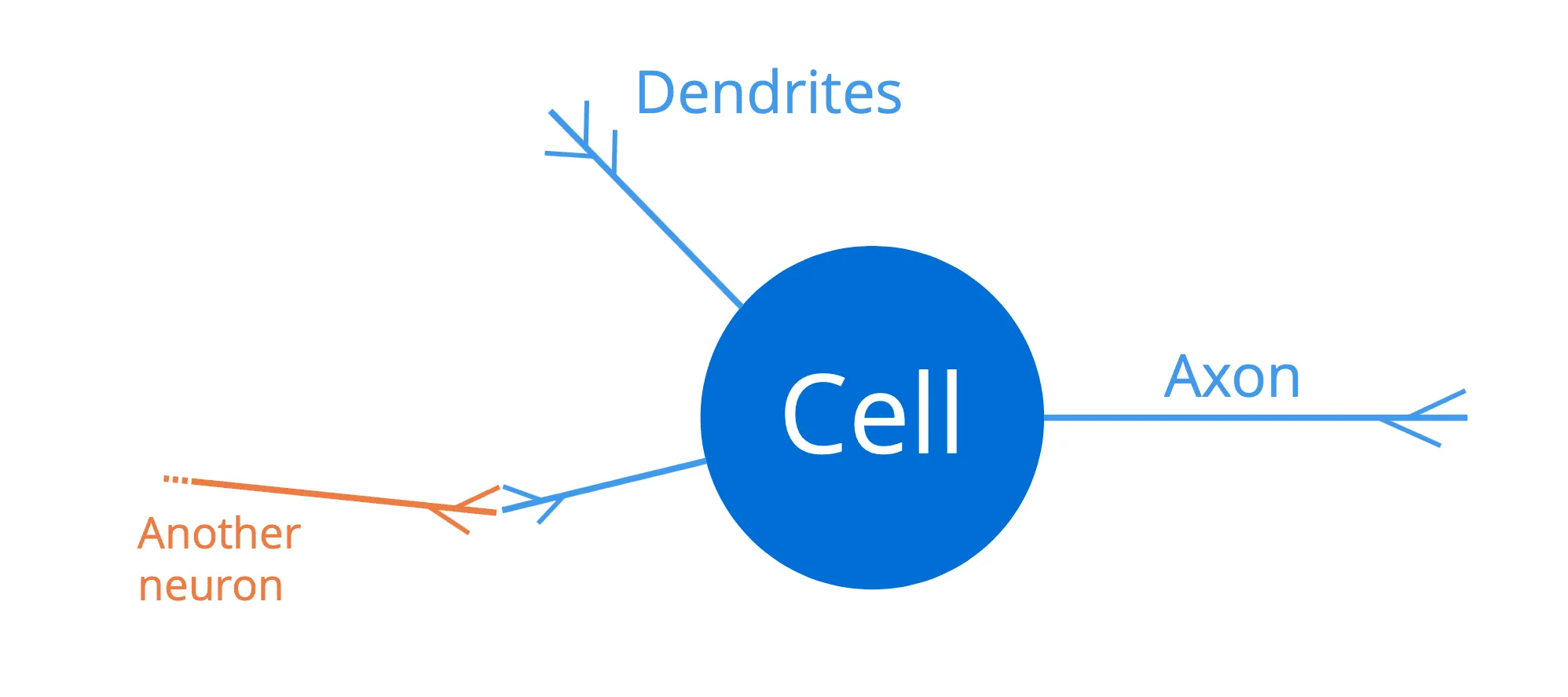
Dendrit bertindak sebagai saluran input ke neuron, sedangkan akson bertindak sebagai saluran output. Oleh karena itu, sebuah neuron akan menerima sinyal input melalui dendritnya, yang pada gilirannya akan terhubung ke akson (output) dari neuron lain yang berdekatan. Dengan cara ini, pulsa listrik yang cukup kuat (juga disebut potensial aksi) dapat ditransmisikan di sepanjang akson satu neuron, ke semua neuron lain yang terhubung dengannya. Hal ini memungkinkan sinyal disebarkan di sepanjang struktur otak manusia.

Neural network dapat dianalogikan dengan struktur otak manusia, karena (1) neural network juga terdiri dari sejumlah besar neuron yang saling berhubungan yang, (2) berusaha menyebarkan informasi di seluruh jaringan dengan, (3) menerima serangkaian rangsangan dari neuron-neuron yang berdekatan dan memetakannya menjadi output, untuk kemudian diumpankan ke lapisan neuron berikutnya.

Struktur neural network biasanya disusun ke dalam lapisan-lapisan neuron. Sebagai contoh, diagram berikut ini mengilustrasikan neural network yang terhubung sepenuhnya, di mana semua neuron dalam satu lapisan terhubung ke semua neuron di lapisan berikutnya:

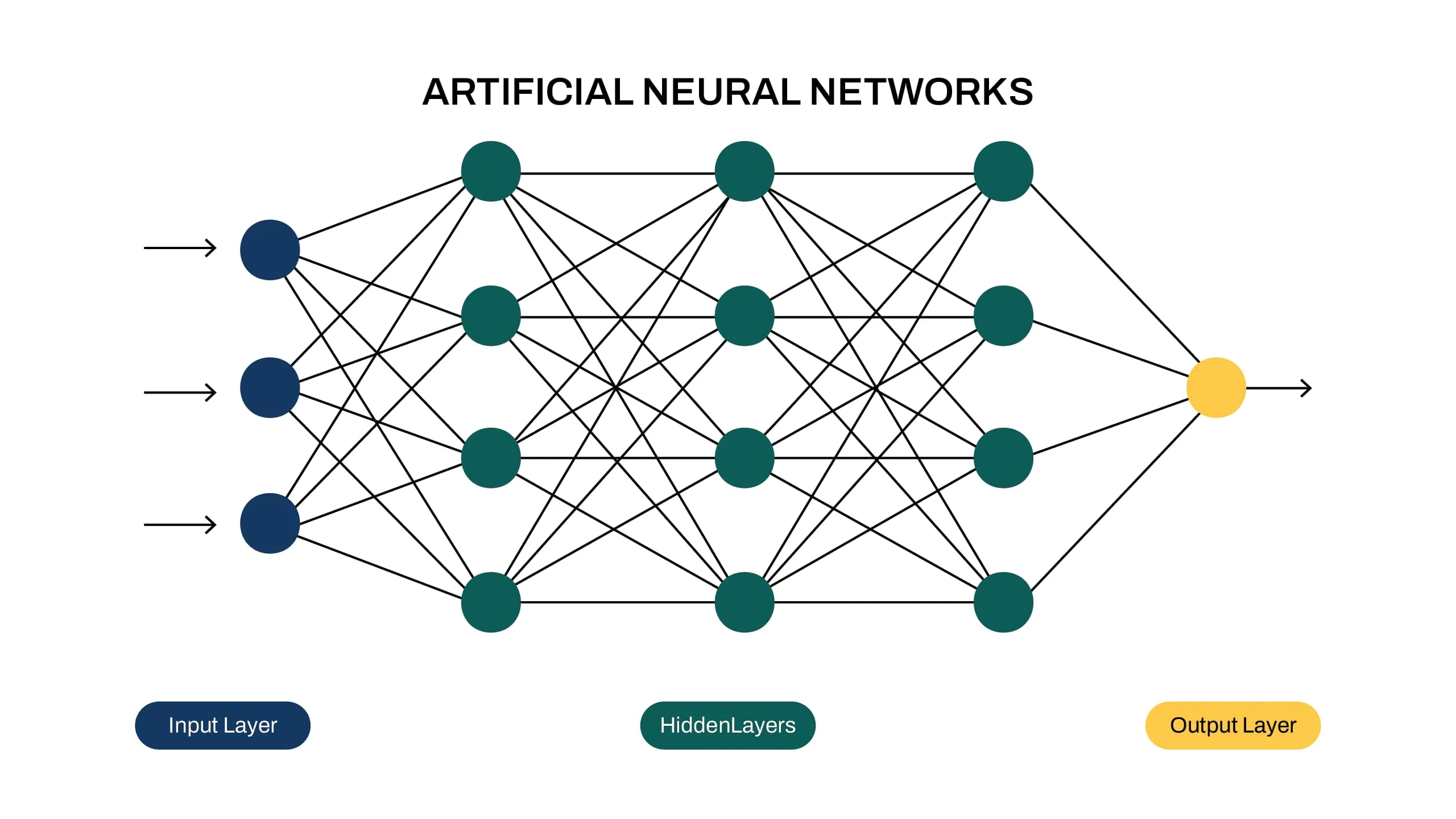
Input disajikan di sisi kiri jaringan, dan informasi merambat (atau mengalir) ke kanan menuju output di ujung yang berlawanan. Karena informasi, dengan ini, merambat ke arah depan melalui jaringan, maka kita juga akan menyebut jaringan seperti itu sebagai neural network feedforward.

Lapisan neuron di antara lapisan input dan output disebut lapisan tersembunyi, karena tidak dapat diakses secara langsung. Setiap koneksi (diwakili oleh panah dalam diagram) antara dua neuron dikaitkan dengan bobot, yang bekerja pada data yang mengalir melalui jaringan, seperti yang akan kita lihat sebentar lagi.

Matematika dari sebuah Neuron#

Sebuah neuron buatan tertentu (atau perceptron, seperti yang awalnya dinamai oleh Frank Rosenblatt) menerima n input, $[x_1, ..., x_n]$, di mana setiap koneksi dikaitkan dengan bobot yang sesuai, $[w_1, ..., w_n]$. Operasi pertama yang dilakukan adalah mengalikan nilai input dengan bobot yang sesuai, dan menambahkan istilah bias, b, pada penjumlahannya, menghasilkan output, z:

$z = (\sum_{i=1}^{n} w_i x_i) + b = ((w_1 \times x_1) + ... + (w_n \times x_n)) + b$

Perhitungan jumlah tertimbang yang telah kita lakukan sejauh ini adalah operasi linier. Jika setiap neuron harus mengimplementasikan perhitungan khusus ini sendirian, maka jaringan syaraf akan dibatasi untuk hanya mempelajari pemetaan input-output linear. Oleh karena itu, operasi kedua dilakukan oleh setiap neuron yang mengubah jumlah terbobot dengan penerapan fungsi activation nonlinier, g(.):

$output = g(z) = g((\sum_{i=1}^{n} w_i x_i) + b)$

Kita dapat merepresentasikan operasi yang dilakukan oleh setiap neuron dengan lebih ringkas lagi, jika kita mengintegrasikan istilah bias ke dalam penjumlahan sebagai bobot lain, $w_0$ (perhatikan bahwa penjumlahan sekarang dimulai dari 0):

$output = g(\sum_{i=0}^{n} w_i x_i)$

Operasi yang dilakukan oleh setiap neuron dapat diilustrasikan sebagai berikut:

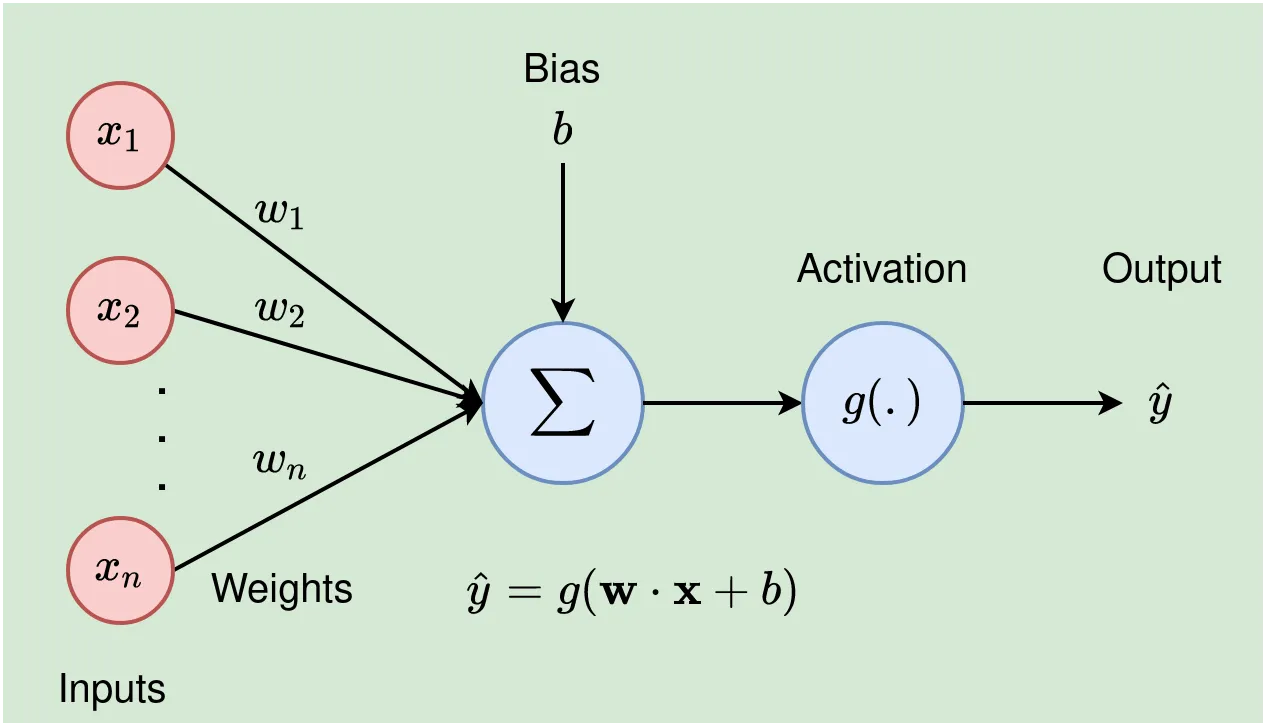
Oleh karena itu, setiap neuron dapat dianggap mengimplementasikan fungsi nonlinier yang memetakan sekumpulan input ke activation output.

Training a Neural Network#

Melatih neural network melibatkan proses pencarian set bobot yang paling sesuai dengan pola dalam data. Ini adalah proses yang menggunakan algoritma backpropagation dan gradient descent secara bersamaan. Kedua algoritma ini menggunakan kalkulus secara ekstensif.

Setiap kali network dilalui ke arah depan (atau ke kanan), kesalahan network dapat dihitung sebagai perbedaan antara output yang dihasilkan oleh network dan kebenaran dasar yang diharapkan, dengan menggunakan fungsi kerugian (seperti jumlah kesalahan kuadrat (SSE)). Algoritma backpropagation, kemudian, menghitung gradien (atau tingkat perubahan/the rate of change) dari kesalahan ini terhadap perubahan bobot. Untuk melakukannya, dibutuhkan penggunaan aturan rantai dan turunan parsial.

Untuk lebih mudahnya, pertimbangkan sebuah network yang terdiri dari dua neuron yang dihubungkan oleh satu jalur activation. Jika kita harus memecahnya, kita akan menemukan bahwa neuron-neuron tersebut melakukan operasi-operasi berikut ini secara bertingkat:

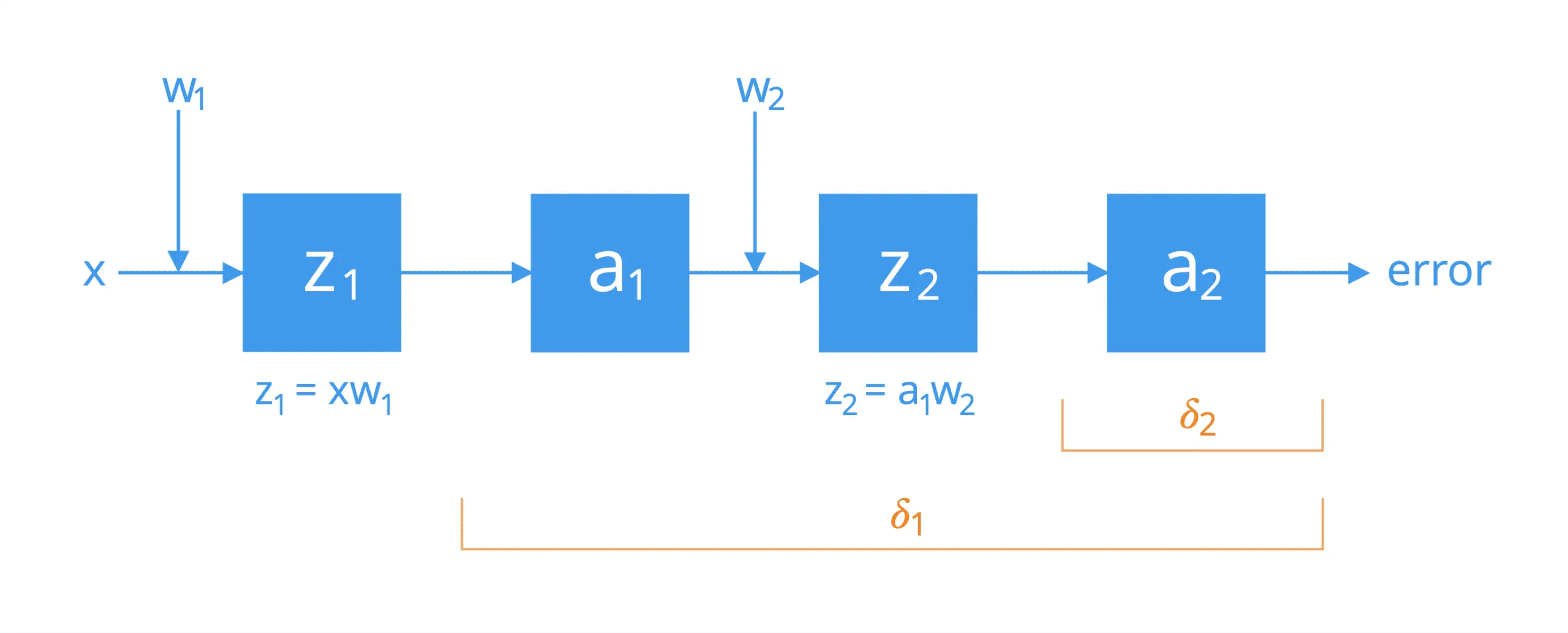
Aplikasi pertama dari aturan rantai (chain rule) menghubungkan kesalahan keseluruhan jaringan ke input, $z_2$, dari fungsi aktivasi $a_2$ dari neuron kedua, dan selanjutnya ke bobot, $w_2$, sebagai berikut:

$\frac{\partial E_{total}}{\partial w_2} = \frac{\partial E_{total}}{\partial a_2} \times \frac{\partial a_2}{\partial z_2} \times \frac{\partial z_2}{\partial w_2} = \partial_2 \times \frac{\partial z_2}{\partial w_2}$

Anda mungkin memperhatikan bahwa penerapan aturan rantai melibatkan, di antara istilah-istilah lainnya, perkalian dengan turunan parsial dari fungsi aktivasi neuron sehubungan dengan inputnya, z2. Ada beberapa fungsi aktivasi yang dapat dipilih, seperti fungsi sigmoid atau fungsi logistik. Jika kita mengambil fungsi logistik sebagai contoh, maka turunan parsialnya akan dihitung sebagai berikut:

$\frac{\partial a_2}{\partial z_2} = \frac{logistic(z)}{\partial z_2} = logistic(z_2) \times (1 - logistic(z_2))$

Oleh karena itu, kita dapat menghitung $\delta_2$ sebagai berikut:

$\delta_2 = \frac{\partial E_{total}}{\partial a_2} \times \frac{\partial a_2}{\partial z_2} = logistic(z_2) \times (1 - logistic(z_2)) \times (t_2 - a_2)$

Di sini, $t_2$ adalah aktivasi yang diharapkan, dan dalam mencari perbedaan antara $t_2$ dan $a_2$, kita menghitung kesalahan antara aktivasi yang dihasilkan oleh jaringan dan kebenaran dasar yang diharapkan.

Karena kita menghitung turunan dari fungsi aktivasi, maka turunan tersebut haruslah kontinu dan dapat dibedakan di seluruh ruang bilangan real. Dalam kasus jaringan syaraf tiruan dalam, gradien kesalahan disebarkan ke belakang melalui sejumlah besar lapisan tersembunyi. Hal ini dapat menyebabkan sinyal kesalahan berkurang dengan cepat menjadi nol, terutama jika nilai maksimum fungsi turunannya sudah kecil (misalnya, kebalikan dari fungsi logistik memiliki nilai maksimum 0,25). Hal ini dikenal sebagai masalah gradien lenyap. Fungsi ReLU telah sangat populer digunakan dalam deep learning untuk mengatasi masalah ini, karena turunannya di bagian positif dari domainnya sama dengan 1.

Bobot berikutnya backwards lebih dalam ke dalam jaringan dan, oleh karena itu, penerapan aturan rantai juga dapat diperluas untuk menghubungkan kesalahan keseluruhan ke bobot, $w_1$, sebagai berikut:

$\frac{\partial E_{total}}{\partial w_1} = \frac{\partial E_{total}}{\partial a_2} \times \frac{\partial a_2}{\partial z_2} \times \frac{\partial z_2}{\partial a_1} \times \frac{\partial a_1}{\partial z_1} \times \frac{\partial z_1}{\partial w_1} = \delta_1 \times \frac{\partial z_1}{\partial w_1}$

Jika kita mengambil fungsi logistik lagi sebagai fungsi aktivasi pilihan, maka kita akan menghitung $\delta_1$ sebagai berikut:

$\delta_1 = \frac{\partial E_{total}}{\partial a_2} \times \frac{\partial a_2}{\partial z_2} \times \frac{\partial z_2}{\partial a_1} \times \frac{\partial a_1}{\partial z_1} = \delta_2 \times \frac{\partial z_2}{\partial a_1} \times \frac{\partial a_1}{\partial z_1} = \delta_2 \times w_2 \times logistic(z_1) \times (1 - logistic(z_1))$

Setelah kita menghitung gradien dari kesalahan jaringan sehubungan dengan setiap bobot, maka algoritma gradient descent dapat diterapkan untuk memperbarui setiap bobot untuk perambatan maju berikutnya pada waktu, t+1. Untuk bobot, $w_1$, aturan pembaruan bobot menggunakan gradient descent akan ditentukan sebagai berikut:

$w_1(t+1) = w_1(t) - \eta \times \frac{\partial E_{total}}{\partial w_1}$

Meskipun kita telah mempertimbangkan sebuah jaringan sederhana, proses yang telah kita lalui dapat diperluas untuk mengevaluasi jaringan yang lebih kompleks dan lebih dalam, seperti jaringan syaraf tiruan (CNN).

Jika jaringan yang sedang dipertimbangkan memiliki banyak cabang yang berasal dari banyak input (dan mungkin mengalir ke beberapa output), maka evaluasinya akan melibatkan penjumlahan rantai turunan yang berbeda untuk setiap jalur, mirip dengan bagaimana kita telah menurunkan aturan rantai yang digeneralisasi sebelumnya.

Summary#

Dalam tutorial ini, Anda telah menemukan bagaimana aspek kalkulus diterapkan dalam jaringan syaraf. Secara khusus, Anda telah belajar:

• Jaringan saraf tiruan disusun ke dalam lapisan neuron dan koneksi, di mana setiap neuron dan koneksi diberi nilai bobot.
• Setiap neuron mengimplementasikan fungsi nonlinier yang memetakan sekumpulan input ke aktivasi output.
• Dalam melatih jaringan saraf, kalkulus digunakan secara ekstensif oleh algoritme backpropagation dan gradient descent.